公倍数求解

在初中数学中，公倍数是一个非常常见的概念。任何两个数都有公倍数，但如何快速而准确地求出它们的公倍数却是不少同学头疼的问题。

本文将介绍几种快速求解公倍数的技巧，希望能够帮助大家更好地理解和掌握这一内容。

方法一：分解质因数法

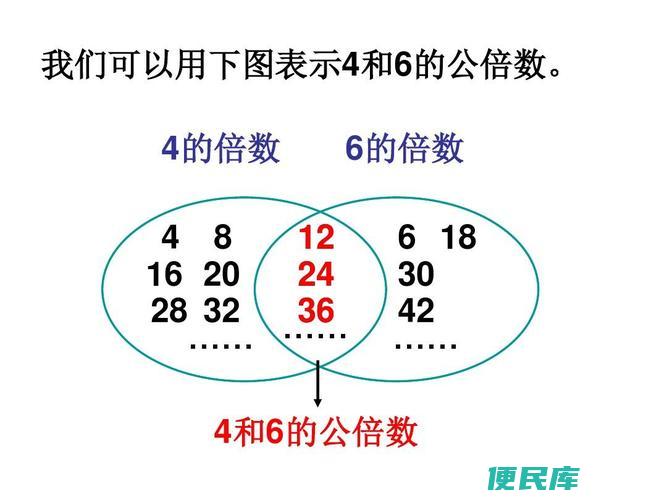
分解质因数是初中数学中比较基础的知识点，它能够将一个数分解为若干个质数的乘积形式。利用这一方法，我们可以比较容易地求出任何两个数的最小公倍数。

以求解24和36的最小公倍数为例：

首先，分别对24和36分解质因数，得到：

24=2×2×2×3

36=2×2×3×3

接下来，我们把不同的质因数列出来，再分别找出两个数中的最大次数，最后将这些质因数和对应的最大次数相乘即可。具体来说，我们可以得到以下计算过程：

24= 2×2×2×3

36= 2×2×3×3

最小公倍数= 2×2×2×3×3=72

由此可见，分解质因数法是一种比较简单而又有效的求解公倍数的方法。但需要注意的是，当数值过于庞大时，分解质因数将变得十分困难。

方法二：辗转相除法

辗转相除法是又一个常见的求解最小公倍数的方法，它的核心思想是基于两个数的最大公约数来计算最小公倍数。

因为对于两个数a和b来说，它们的最小公倍数lcm(a,b)等于它们的乘积ab除以最大公约数gcd(a,b)。

以求解24和36的最小公倍数为例，我们可以用辗转相除法计算出它们的最大公约数，然后再根据最大公约数反推出最小公倍数：

（1）用辗转相除法求解最大公约数

24和36的公因数有1、2、3、4、6、8、12，其中6是它们的最大公约数。

（2）根据最大公约数求解最小公倍数

24和36的最小公倍数=24×36÷6=144

可以看出，辗转相除法比分解质因数法更适合解决大数的最小公倍数问题，但需要注意的是，它的计算过程稍微有点繁琐，需要正确理解其思路和计算方法才能得到正确答案。

方法三：公式法

公式法是又一种比较实用而又简单的求解公倍数的方法。

它的基本思路是利用两个数之积等于它们的最大公约数与最小公倍数之积来计算最小公倍数。具体来说，其公式为：

lcm(a,b)=ab÷gcd(a,b)

其中gcd(a,b)代表a和b的最大公约数，ab代表a和b的乘积，÷为除号。

以求解24和36的最小公倍数为例，我们可以根据公式直接得出它们的最小公倍数：

lcm(24,36)=24×36÷gcd(24,36)=24×36÷6=144

可以看出，公式法是比较快捷而又实用的求解公倍数的方法，它不需要进行分解质因数或辗转相除等繁琐运算，可以直接使用公式求解。

总结

综上所述，求解公倍数是数学中比较基础和实用的知识点，常常用于分数化简、比较大小等，因此掌握其求解方法是十分重要的。

本文介绍了三种常用的公倍数求解方法：分解质因数法、辗转相除法和公式法。

这三种方法各有优劣，具体使用应根据数据规模、时间限制和实际情况等综合考虑，选用合适的方法来求解公倍数

最后，关于本文标题“公倍数求解”的问题，可以简单回答为：公倍数可以使用分解质因数、辗转相除或公式等方法进行求解。

标签： 公倍数、 求解、 技巧、 快速、

本文地址： https://www.bminku.com/bmxx/6e180b2f003c1b8f7b89.html

上一篇：创建电子邮件快速创建个人电子邮件的步骤...
下一篇：内六角螺丝滑丝了怎么取出来取出滑丝六角螺...