什么是对角矩阵？

在线性代数中，对角矩阵是一种特殊的方阵，其主对角线上的元素为非零，而其余元素均为零。对于一个n×n的对角矩阵，可以表示为一个对角线上有n个元素的向量，而每个元素就是对角线上的一个数。

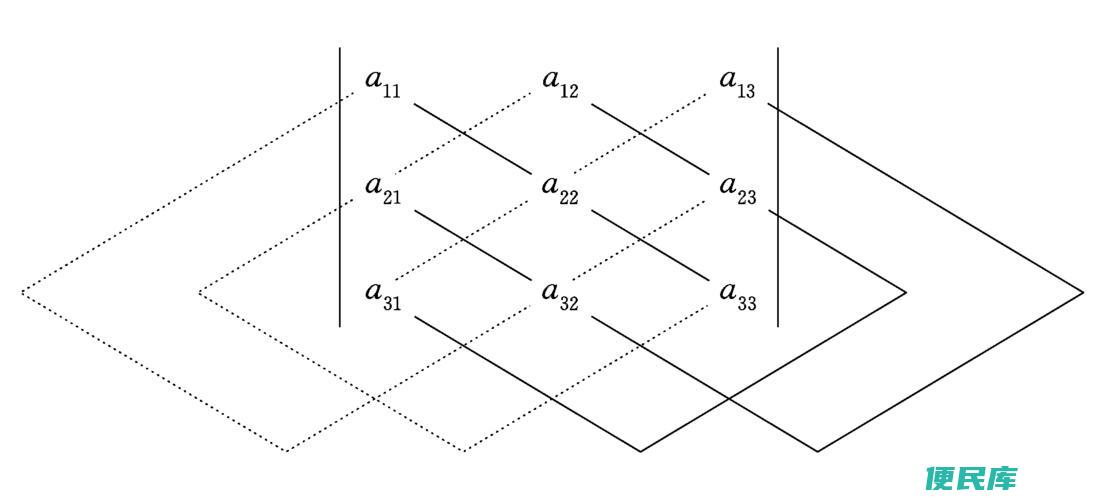
举个例子，我们可以将自然数1到9按照如下方式排列成一个3×3的矩阵：

\begin{bmatrix}

\end{bmatrix}

这是一个对角矩阵，其主对角线上的元素分别为1、5和9。

对角矩阵的特点

对角矩阵具有很多有用的特性，这些特性使得对角矩阵在许多应用中经常出现。

乘法运算容易

对角矩阵的乘法运算非常容易。对于两个对角矩阵A和B，它们的乘积为：

AB = \begin{bmatrix}

a_{1} & 0 & 0 \\

0 & a_{2} & 0 \\

\end{bmatrix}

\begin{bmatrix}

b_{1} & 0 & 0 \\

0 & b_{2} & 0 \\

\end{bmatrix} =

\begin{bmatrix}

a_{1}b_{1} & 0 & 0 \\

0 & a_{2}b_{2} & 0 \\

0 & 0 & a_{3}b_{3}

\end{bmatrix}

可以看出，乘积中的每个元素都是由两个对角矩阵相应位置上的元素相乘得到的。由于对角矩阵上大部分元素都为零，因此实际的计算量非常小。

行列式为主对角线元素之积

对于一个n×n的对角矩阵，其行列式为主对角线上的元素之积。即：

$$ det(A) = \prod_{i=1}^{n} a_{ii} $$

这个特性使得对角矩阵的行列式非常容易计算。

特征值为主对角线元素

对于一个n×n的对角矩阵，其特征值为主对角线上的元素。即：

$$ Av = \lambda v $$

其中，A是一个对角矩阵，v是它的特征向量，λ是它的特征值。由于对角矩阵上的非零元素只在主对角线上，因此每个特征向量都是由一个单位向量组成。这个特性使得计算对角矩阵的特征值和特征向量非常容易。

逆矩阵为对角线上每个元素的倒数构成的矩阵

对于一个n×n的对角矩阵A，如果它的主对角线上的元素都不为零，那么它的逆矩阵B为：

$$ B = \begin{bmatrix}

\frac{1}{a_{1}} & 0 & 0 \\

0 & \frac{1}{a_{2}} & 0 \\

0 & 0 & \frac{1}{a_{3}}

\end{bmatrix} $$

可以看出，逆矩阵也是一个对角矩阵，其中每个元素都是对应位置上原矩阵元素的倒数。需要注意的是，如果对角矩阵上的某个元素为零，那么这个矩阵就没有逆矩阵。

容易展开成一组正交基

对角矩阵是一个非常好的基向量集合，因为每个基向量都是独立的，并且它们互相正交。由于对角矩阵可以看作是一个由单位向量组成的矩阵，因此很容易将它展开成一组正交基。

容易对角化

对角化是将一个矩阵用对角矩阵表示的过程。对于一个可对角化的矩阵，它必须是一个方阵，并且必须有n个线性无关的特征向量。对角矩阵的特征向量非常容易求解，因此它们也很容易对角化。

总结

对角矩阵是具有很多有用特性的一类矩阵，它们在线性代数和矩阵计算中扮演了重要的角色。对角矩阵的定义很简单，只需要让矩阵的主对角线上的元素为非零值，其余元素为零即可。

特别是对角矩阵的乘法运算非常容易，因为大部分元素都为零，从而减少了计算复杂度。

对角矩阵还具有行列式、特征值、逆矩阵、正交基以及对角化等重要特性，这些特性使得对角矩阵在很多应用领域中都有广泛的应用，如谱聚类、特征向量法、多元计量等等。

标签： 对角矩阵的概念与特点（探讨对角矩阵的定义和特点）、

本文地址： https://www.bminku.com/bmxx/0848e2912384280e398a.html

上一篇：女生回你白眼什么意思女生白眼的表达含义是...
下一篇：固态酒与液态酒差异对比固态酒和液态酒的优...